Arsitektur Komputer+(Assembler)

KOMPLEMEN, FULL ADDER, dan HALF ADDER

Komplemen 1 dan 2 Dan Binary

Dalam komputer terdapat dua buah cara merepresentasikan nilai negatif, yaitu komplemen satu (ones complement) dan komplemen dua (twos complement).

Komplemen satu merupakan suatu sistem penomoran yang diterapkan dalam beberapa jenis komputer untuk merepresentasikan nilai-nilai negatif. Pada cara ini terdapat aturan bahwa nilai 0 (nol) akan direpresentasikan dengan dua buah nilai, yaitu +0 (positif nol) dan -0 (negatif nol).

000…00011 = +3

000…00010 = +2

000…00001 = +1

000…00000 = +0

111…11111 = -0

111…11110  = -1

111…11101 = -2

111…11100 = -3

Dapat kita lihat dari aturan diatas, nilai +0 akan berpasangan dengan -0, +1 dengan -1, dan seterusnya. Ini menunjukkan bahwa negasi dari 0 adalah -0, negasi dari 1 adalah -1, dan seterusnya.

Terdapat kelemahan dalam aturan ini, yaitu ada nilai yang kurang benar sehingga diciptakannya aturan ke dua yaitu komplemen dua.

Komplemen dua mirip dengan komplemen satu, hanya saja dalam proses negasinya semua bit juga akan dibalik, sehingga tidak ada lagi rasa “bingung” merepresentasikan nilai +0 dan -0, karena hanya ada satu nilai 0 (nol), seperti berikut:

000…00011 = +3

000…00010 = +2

000…00001 = +1

000…00000 = 0

111…11111 = -1

111…11110 = -2

111…11101 = -3

111…11100 = -4

dari aturan di atas dapat kita lihat bahwa nilai 0 akan berpasangan dengan nilai -1, nilai +1 akan berpasangan dengan -2, dan seterusnya. Hal ini menunjukkan bahwa negasi dari 0 adalah -1, negasi dari +1 adalah -2, dan begitu seterusnya.

Sistem bilangan binari menggunakan basis (radix) 2 dan menggunakan dua macam simbol yaitu : 0 dan 1. Contoh bilangan binari yaitu : 1001 dapat diartikan dalam sistem bilangan desimal yaitu :

 

Position value sistem bilangan binari merupakan perpangkatan dari nilai basis yaitu perpangkatan nilai 2, seperti pada tabel berikut :

Atau dengan rumus :

Contoh :

Pertambahan Bilangan Binari

Pertambahan bilangan binari dilakukan dengan cara yang sama dengan pertambahan bilangan desimal. Dasar pertambahan untuk masing-masing digit bilangan binari adalah :

Contoh pertambahan bilangan binari :

Pengurangan Bilangan Binari

Pengurangan pada sistem bilangan binari dilakukan dengan cara yang sama pada sistem bilangan desimal. Dasar pengurangan untuk masing-masing digit bilangan adalah :

Contoh pengurangan pada sistem bilangan binari :

Pengurangan Dengan Komplemen (Complement)

Komplemen basis minus 1 (radix-minus-one complement)

Komplemen basis (radix complement)

Pada sistem bilangan desimal :

Kompelemen 9 (9s complement)

Komplemen 10 (10s complement)

Pada sistem bilangan binari :

Komplemen 1 (1s complement)

Komplemen 2 (2s complement)

Contoh pengurangan dengan komplemen 9 :

Komplemen 9 dari suatu sistem bilangan desimal dilakukan dengan mengurangkan angka 9 untuk masing-masing digit dalam bilangan pengurangan. Perhatikan, pada komplemen 9, digit paling ujung kiri dipindahkan untuk ditambahkan pada digit paling kanan.

Contoh pengurangan dengan komplemen 10 :

Komplemen 10 dari bilangan desimal adalah hasil komplemen 9 ditambah 1, misalnya komplemen 10 dari nilai 321 adalah 679 (atau dengan cara 1000-321 = 679). Pada komplemen 10, hasil digit paling ujung kiri dibuang (tidak dipergunakan).

Cara yang sama dapat dilakukn pada sistem bilangan binari.

Contoh pengurangan dengan komplemen 1 :

Komplemen 1 di sistem bilangan binari dilakukan dengan mengurangkan setiap bit dari nilai 1, atau dengan cara mengubah setiap bit 0 menjadi 1 dan bit 1 menjadi 0. Dengan komplemen 1, hasil digit paling kiri dipindahkan untuk ditambahkan pada bit paling kanan.

Contoh pengurangan dengan komplemen 2 :

Komplemen 2 adalah hasil dari komplemen 1 ditambah 1, misalnya komplemen 2 dari bilangan binari 10110 adalah 01010 (dari komplemen 1 yaitu 01001 ditambah 1). Dengan komplemen 2, hasil digit paling kiri dibuang (tidak digunakan).

Perkalian Bilangan Binari

Perkalian bilangan binari dilakukan dengan cara yang sama dengan perkalian pada sistem bilangan desimal. Dasar perkalian untuk masing-masing digit bilangan binari adalah :

Contoh perkalian bilangan binari :

Perhatikan, ada 2 keadaan dalam perkalian bilangan biner, jika pengali adalah bilangan 1, maka cukup disalin saja, jika pengali adalah bilangan 0, maka hasilnya semuanya 0.

Pembagian Bilangan Binari

Pembagian pada bilangan binari dilakukan dengan cara yang sama dengan pembagian bilangan desimal. Pembagian dengan 0 tidak mempunyai arti, sehingga dasar pembagian digit binari adalah :

Contoh pembagian bilangan binari :

Half Adder

Dengan bantuan dari setengah adder, kita dapat merancang sirkuit yang mampu melakukan penambahan sederhana dengan bantuan gerbang logika.

Mari kita melihat penambahan bit tunggal.

0 +0 = 0

0 +1 = 1

1 +0 = 1

1 +1 = 10

Ini adalah paling mungkin kombinasi single-bit. Tapi hasil untuk 1 +1 adalah 10. Meskipun masalah ini dapat diselesaikan dengan bantuan sebuah gerbang EXOR, jika Anda peduli tentang output, hasil penjumlahan harus ditulis ulang sebagai output 2-bit.

Dengan demikian persamaan di atas dapat ditulis sebagai

0 +0 = 00

0 +1 = 01

1 +0 = 01

1 +1 = 10

Berikut output '1 'dari '10' menjadi membawa-out. Hasilnya akan ditampilkan dalam kebenaran-tabel di bawah ini. 'SUM' adalah output normal dan 'BAWA' adalah membawa keluar.

INPUT OUTPUT

Sebuah SUM B BAWA

0 0 0 0

0 1 1 0

1 0 1 0

1 1 0 1

Dari persamaan itu jelas bahwa ini adder 1-bit dapat dengan mudah diimplementasikan dengan bantuan EXOR gerbang untuk output 'SUM' dan DAN gerbang untuk carry. Lihatlah implementasi di bawah ini.

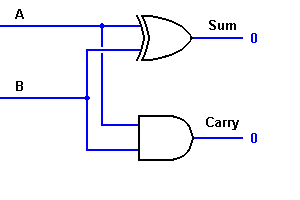
Half Adder Circuit

Untuk Selain itu kompleks, mungkin ada kasus ketika Anda harus menambahkan dua byte 8-bit bersama-sama. Hal ini dapat dilakukan hanya dengan bantuan logika penuh penambah.

Full Adder

Jenis penambah adalah sedikit lebih sulit untuk diterapkan daripada setengah-penambah. Perbedaan utama antara setengah-penambah dan penuh Adder adalah bahwa penuh Adder memiliki tiga input dan dua output.Pertama kedua input A dan B dan masukan ketiga adalah input membawa ditunjuk sebagai CIN. Ketika logika adder penuh dirancang kita akan mampu ke string delapan dari mereka bersama-sama untuk menciptakan penambah byte-lebar dan kaskade bit carry dari satu penambah ke yang berikutnya.

Output membawa ditunjuk sebagai COUT dan output normal ditetapkan sebagai S. Lihatlah kebenaran-tabel.

INPUT OUTPUT

A B CIN COUT S

0 0 0 0 0

0 0 1 0 1

0 1 0 0 1

0 1 1 1 0

1 0 0 0 1

1 0 1 1 0

1 1 0 1 0

1 1 1 1 1

Dari atas kebenaran tabel, logika penambah penuh dapat diimplementasikan. Kita bisa melihat bahwa output S adalah EXOR antara input A dan SUM keluaran setengah-penambah dengan B CIN input. Kita juga harus mencatat bahwa COUT hanya akan benar jika salah satu dari dua input dari tiga yang TINGGI.

Dengan demikian, kita dapat menerapkan sirkuit adder penuh dengan bantuan dua setengah sirkuit adder.Yang pertama akan setengah adder akan digunakan untuk menambah A dan B untuk menghasilkan Sum parsial. Babak kedua logika adder dapat digunakan untuk menambah CIN ke Sum dihasilkan oleh setengah adder pertama untuk mendapatkan output S akhir. Jika salah satu setengah logika adder menghasilkan sebuah carry, akan ada output carry. Dengan demikian, COUT akan menjadi fungsi OR dari output Carry half-adder. Lihatlah pelaksanaan rangkaian adder penuh ditunjukkan di bawah ini.

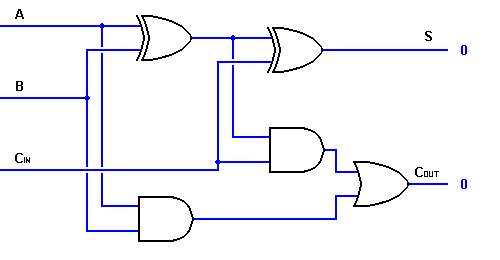
Penuh Adder Circuit

Meskipun pelaksanaan diagram logika yang lebih besar dimungkinkan dengan logika penambah penuh atas simbol sederhana banyak digunakan untuk mewakili operasi. Diberikan di bawah ini adalah representasi skematis sederhana penuh adder satu-bit.

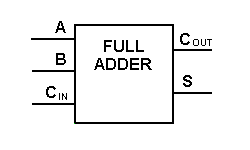
Single-bit Adder Penuh

Dengan jenis simbol, kita dapat menambahkan dua bit bersama-sama mengambil carry dari selanjutnya agar lebih rendah besarnya, dan mengirim membawa kepada tatanan yang lebih tinggi berikutnya besarnya.Dalam komputer, untuk operasi multi-bit, setiap bit harus diwakili oleh penambah penuh dan harus ditambahkan secara bersamaan. Dengan demikian, untuk menambahkan dua angka 8-bit, Anda akan membutuhkan 8 penambah penuh yang dapat dibentuk dengan cascading dua blok 4-bit. Penambahan dua angka 4-bit ditunjukkan di bawah ini.

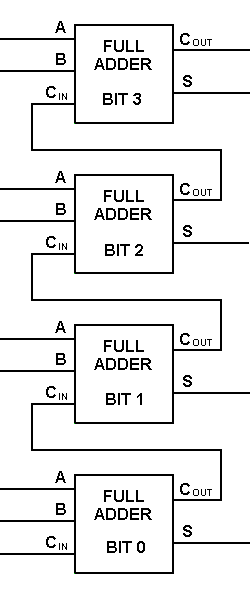
Penambahan Multi-Bit menggunakan Full Adder

Representasi Data

Bilangan desimal, Bilangan biner, Bilangan oktal, dan Bilangan heksadesimal

Bilangan Desimal : Bilangan yang menggunakan 10 angka mulai 0 sampai 9 berturut2.

Bilangan Biner : Bilangan yang hanya menggunakan 2 angka, yaitu 0 dan 1.

Bilangan Oktal : Bilangan berbasis 8, yang menggunakan angka 0 sampai 7.

Bilangan Heksadesimal : Bilangan yang menggunakan 16 buah simbol, mulai dari 0-9, kemudian dari A-F

Konversi Bilangan Desimal, Biner, Oktal, dan Heksadesimal

Misalkan bilangan desimal yang ingi saya konversi adalah 25 ₁₀. Maka langkah tersebut dibagi dengan 2 seperti berikut: 25 : 2 = 12,5 jawabannya memang benar, tapi bukan tahapan ini yang kita ingingkan.

Tahapan yang tepat sbg : 25 : 2 = 12 sisa 1

Langkah selanjutnya membagi angka 12 dengan 2 lagi, jadi :12 : 2 =6 sisa 0

•          Konversi desimal ke heksadesimal

Proses konversinya mirip dengan proses konversi desimal ke biner, hanya saja pembaginya adalah 8.

Misalkan angka konversi adalah 33 ₁₀. Maka :

                33 : 8 = 4 sisa 1

                4 : 8 = 0 sisa 4

                0 : 8 = 0 sisa 0….(end)

                Maka hasil konversinya adalah 41 ₈

•          Konversi bilangan biner ke desimal

Proses konversi bilangan biner ke bilangan desimal adalah proses perkalian setiap bit pada bilangan biner dengan perpangkatan 2, dimana perpangkatan 2 tersebut berurut dari kanan ke kiri bit bernilai 2⁰ sampai 2ⁿ. Hasil perhitungannya adalah 11001₂

                1     ——>    1 x 2⁰ = 1

                0     ——>    0 x 2¹ = 0

                0     ——>    0 x 2² = 0

                1     ——>    1 x 2³ = 8

              1     ——>    1 x 2⁴ = 16 —> perhatikan nilai perpangkatan 2 nya semakin ke bawah semakin besar.

                Maka hasilnya adalah 1 + 0 + 0 + 8 + 16 = 25₁₀.

•          Konversi bilangan biner ke oktal

Untuk merubah bilangan biner ke bilangan oktal, perlu diperhatikan bahwa setiap bilangan oktal mewakili 3 bitdari bilangan biner.

                Contoh: konversikan 10110011₂ ke bilangan oktal

                Jawab : 10  110  011

                    2      6     3

                Jadi 10110011₂ = 263₈

•          Konversi bilangan biner ke heksadesimal           

Proses konversinya juga tidak begitu rumit, hanya tinggal memilahkan bit2 tersebut menjadi kelompok2 4 bit.

                Contoh: konversikan 10110011₂ ke bilangan heksadesimal

                Jawab : 1011  0011

                               B       3

                                                Jadi 10110011₂ = B3₁₆

•          Konversi bilangan oktal ke desimal        

Hal ini tidak terlalu sulit. Tinggal kalikan saja setiap bilangan dengan perpangkatan 8. Contoh, bilangan oktal yang akan dikonversi adalah 71₈. Maka susunannya saya buat menjadi demikian :

                1 x 8⁰ = 1

                7 x 8¹ = 56

                                                Maka hasilnya adalah penjumlahan 1 +                  56 = 57₁₀.

•          Konversi bilangan oktal ke biner

Untuk mengkonversi Bilangan Oktal ke Biner yang harus dilakukan adalah terjemahkan setiap digit bilangan oktal ke 3 digit bilangan biner.

                Contoh Konversikan 263₈ ke bilangan biner.

                Jawab:  2       6      3

                     010   110   011

                                                Jadi 263₈ = 010110011₂ Karena 0 didepan tidak ada artinya kita bisa menuliskan 10110011₂

•          Konversi bilangan oktal ke heksadesimal

ü  Untuk konversi oktal ke heksadesimal, kita akan membutuhkan perantara, yaitu bilangan biner. Maksudnya?

ü  Maksudnya adalah kita konversi dulu oktal ke biner, lalu konversikan nilai biner tersebut ke nilai heksadesimalnya.

ü  Nah, baik yang konversi oktal ke biner maupun biner ke heksadesimal kan udah dijelaskan.

ü  Coba buktikan, bahwa bilangan oktal 72₈ jika dikonversi ke heksadesimal menjadi 3A₁₆.

               

 •          Konversi bilangan heksadesimal ke desimal

Untuk proses konversi ini, caranya sama saja dengan proses konversi biner ke desimal, hanya saja kali ini perpangkatan yang digunakan adalah perpangkatan 16, bukan perpangkatan 2.

                contoh :  C8₁₆

                        8 x 16⁰ = 8

                C x 16¹ = 192     ——> ingat, C₁₆ merupakan lambang dari 12₁₀

                                                                        Maka diperolehlah hasil konversinya bernilai   8 + 192 = 200₁₀.

•          Konversi bilangan heksadesimal ke biner

Sebaliknya untuk mengkonversi Bilangan Hexadesimal ke Biner yang harus dilakukan adalah terjemahkan setiap digit bilangan Hexadesimal ke 4 digit bilangan biner.

                Contoh Konversikan B3₁₆ ke bilangan biner.

                Jawab:   B       3

                1011   0011

                                                 Jadi B3₁₆ = 10110011₂

ARSITEKTUR KOMPUTER

Pengertian Mainboard Berserta Gambar, Komponen Dan Fungsi

Seperti yang kita tahu bahwa komponen hardware ada yang disebut Central

Processing Unit (CPU). CPU merupakan otak dari komputer yang menjadi kendali utama

komputer. Terdapat banyak komponen-komponen didalamnya, salah satunya adalah

Mainboard atau Motherboard. Dikatakan demikian karena Mainboard merupakan

komponen atau elemen utama yang ada dalam CPU. Mainboard merupakan papan sirkuit

yang digunakan untuk meletakan komponen-komponen CPU untuk pemasangan

hardware. Seperti yang dipaparkan fungsi Mainboard adalah sebagai media tempat untuk

menghubungkan komponen-komponen hardware agar komputer dapat bekerja, juga

merupakan media terbesar yang ada dalam CPU. Pada Mainboard terpasang pula kabel

penghubung dari Power Supply, kabel tersebut yang memberikan sumber arus listrik agar

Mainboard dapat bekerja.

Papan Induk (Mainboard/Motherboard)

Ok, Sekarang Waktunya mengenal lebih jauh tentang perangkat-perangkat yang ada dalam PC :)

      1. CPU (Central Processing Unit)

CPU adalah central dari semua kegiatan computer seperti halnya otak kita teman-teman, bila CPU ini tidak ada maka computer tidak akan tau apa yang harus dikerjakannya dan bisa dilihat dengan jelas CPU itu di letakan atau dipasang di CPU soket.

Central Processing Unit (CPU).

      2.   RAM (Random Access Memory)

RAM itu adalah tempat penyimpanan data jangka pendek, sehingga computer tidak perlu selalu mengakses hard disk untuk mencari data. Jumlah RAM yang lebih besar akan membantu kecepatan PC dalam beroprasi. Di mainboard RAM dipasang di RAM soket.

Random Acces Memory (RAM).

      3.   VGA (Video Graphics Adapter)

VGA adalah sebuah benda untuk mengolah data graphis dan ditampilkan di layar monitor, VGA juga memiliki processor yang dinamakan GPU(Graphics Processing Unit) dan membutuhkan memory juga.

Video Grafis Adapter (VGA).

VGA terdapat ada dua jenis yaitu AGP dan PCI perbedaannya terletak di kaki VGAnya.

AGP

PCI

      4.   Northbridge

Northbridge itu adalah benda yang mengatur jalannya CPU dan RAM istilahnya northbridge ini controlnya CPU dan RAM.

Northbridge (Jembatan Utara)

Setiap mainboard bentuk northbridgenya pasti beda-beda, tapi fungsinya tetap sama , rata-rata northbridge ini terletak di antara CPU dan RAM.

      5.       Southbridge

Southbridge adalah tempat pengaturnya input output device. Jadi semua yang berhubungan dengan input output diatur oleh southbridge.

Southbridge (Jembatan Selatan)

      6.       Bios Battery
      Kegunaan bios battery itu buat menyimpan settingan bios kita teman-teman.bila bios kita ingin di restart atau   kembali ke tampilan pabrikan battery bios bisa di lepas dulu, lalu dipasang kembali.

Cara lepas battery

      7.       Chip Bios

Kegunaan Chip Bios ini untuk menampilkan bios di layar computer

Chip Bios

      8.       Hard Disk

Hard Disk adalah hardware yang berfungsi sebagai penyimpan data, bila tidak ada hard disk ini computer kita tidak bisa menyimpan data-data yang telah kita masukan ke computer.

Penampakkan dari hard disk ini seperti

Hard Disk ini ada dua tipe yaitu:

 Type ATA

Type S-ATA

Perbedaannya terletak dari kecepatan menginput atau output data dari hard disk, yang S-ATA lebih cepat dari ATA.

      9.       DVD-RW

DVD-RW adalah tempat memutar, membaca, dan membackup data ke disc.

Penampakkan dari DVD-RW ini seperti

DVD-RW

NB: Kalau DVD-RW kita bisa membaca atau membackup data baik disc CD atau DVD. Kalau DVD-R hanya bisa membaca disc CD atau DVD saja dan tidak bisa membackup data. Kalau CD-RW bisa membaca dan membackup CD saja. Kalau CD-R hanya bisa membaca CD saja dan tidak bisa membackup data.

      10.   Power Supply

Power Supply ini sangat penting fungsinya sebagai arus listrik untuk mengoprasikan computer kita berasal dari power Supply ini.

 

Power Supply